Preface

This website contains labs for CSCI 210.

At the top of this page, you’ll find three icons. The left shows or hides the table of contents. The middle one lets you pick a theme for this book (go ahead and pick one you like). The right one lets you search the labs.

Throughout the labs, you’ll find a number of colorful blocks like the example above. Here are a few you’ll encounter in the labs.

Lab 1. Introduction to MIPS

Due: Sunday, February 23 at 23:59

Your task is to write a program which takes in a number and stores it in a four-element array at a user-specified index, then prints the contents of the array. You will write this program using the MARS MIPS simulator, which you can download here.

Preliminaries

First, download MARS (there’s a “Download MARS” button at the top of the page).

If you don’t already have a GitHub account, make one. As a student, you can get additional GitHub benefits such as unlimited private repositories here, but you don’t need to for this course. All of your repositories will be private to you and course instructors.

You’ll need Git installed in order to download and submit assignments. On macOS, Git is included with Xcode which can be installed from the App Store. On Linux, Git can be installed using your distribution’s package manager. You can install any of the many other Git tools instead, including GitHub Desktop on macOS and Windows.

Click on the assignment link.

Once you have accepted the assignment, you can clone the repository on your computer by following the instruction and begin working.

Be sure to ask any questions on Ed.

Program specification

Read two input values from the keyboard:

1. a number to enter in the array; and
2. the index of the array where you should store the first number.

Print out each index of the array, and its contents. It should look like this.

  Please enter a number 6
  Which element of the array would you like this to be? 1
  0: 0
  1: 6
  2: 0
  3: 0

Or like this.

  Please enter a number 3
  Which element of the array would you like this to be? 0
  0: 3
  1: 0
  2: 0
  3: 0

You can assume the user will not input any indexes outside of the bounds of the array. You are required to store the user’s value in memory at the specified position, and to load every value in the array from memory into a register to print it out.

Note that you will need to translate between indices, which are word addresses, and values in memory, which are byte addresses.

Make sure to document your programs thoroughly. (This is especially important in assembly language programs, since the code itself is less easily read than high-level language code.) This should include:

1. A block of comment lines at the beginning of the source file, giving the name and author of the program and a black-box description of what it does.
2. A few comment lines between major sections of the program, describing the contents of each section.
3. A comment at the end of most source lines, describing what the instruction on that line does.

Helpful resources

• A guide to the MARS simulator
• A list of MIPS system calls supported by MARS

Hints

1. You will need to use various system calls to print strings, integers, etc. These are all provided on the list of system calls linked above.
2. The la instruction loads the address of a label. You can use this to load the addresses of any of the variables in the .data section of your code.
3. The mul instruction will allow you to multiply a register by a constant.
4. I have included some strings you may find helpful in the .data section.
5. You do not need to write any loops.
6. Your array must be 4-byte aligned. You can use

   .align 2
   arr: .space 16
   

   to get a 4-byte aligned array.

Submission

Submit the lab by committing your code and pushing it to your GitHub repository. From the command line, you would enter the commands

$ git commit -m "Finished!" lab01.asm
$ git push

from inside your repository’s directory.

The first command instructs Git to take the changes that you made to lab01.asm and record those changes on your computer. Usually, when writing software, you would make multiple commits. This allows you to “easily” go back to previous versions. (“Easily” is in quotes because nothing with Git is ever actually easy.)

The second command instructs Git to take all of the changes that you have committed and push them to your repository on GitHub. You can push each time you commit, or you can push after several commits have been made and all commits that haven’t yet been pushed to GitHub will be pushed at that time.

If you don’t push after committing the final version of your code, the graders will not be able to see your changes (because they’ve only been recorded on your local computer).

Rather than use the command line, you can visit the web page for your repository on GitHub and drag and drop the files on the page. I don’t really recommend doing this; it’s better to learn how to use Git properly. But it does work and you’re welcome to do it.

Lab 2. Bitwise Operations

Due: Sunday, March 2 at 23:59

Your task is to write a Rust program that performs bit operations on integers.

Preliminaries

Click on the assignment link.

Once you have accepted the assignment, you can clone the repository on your computer by following the instruction and begin working.

This lab is in Rust. You’ll either need to have the Rust toolchain installed on your computer (I recommend using rustup) or use the lab machines which have Rust installed.

Be sure to ask any questions on Ed.

Program specification

In the assignment repository you will find a Rust project named bitops. This project contains source code for a library src/lib.rs which you will be editing and a binary src/main.rs which you will not be editing.

Your task is to implement the functions in src/lib.rs. You are only allowed to use the Rust bit operators, & (and), | (or), ^ (xor), >> (right shift), and << (left shift). You will not receive credit for the lab if you use addition, subtraction, division, multiplication, modulo/remainder, or control flow constructs like if and loops.

You must perform bit operations directly on the integer passed to each function, and you are not allowed to convert the integer to another format. In particular, you may not convert the integer to a String. For any method that asks you to change specific bits, you should assume bits are numbered 31 to 0, with 31 being the most significant bit or highest bit, and 0 being the least significant bit or lowest bit. All of these methods can (and should) be implemented with a single line of code.

#![allow(unused)]
fn main() {
fn set_bit_one(x: u32) -> u32 {
    x | 2
}
}

It may be helpful to know that you can specify the value of an integer in hexadecimal by prepending it with 0x, e.g., let x = 0xBADBEEF;. You can also specify the value of an integer in octal by prepending it with 0o or in binary by prepending it with 0b.

The bitops binary whose source code is in src/main.rs takes input in the form of command line arguments. Each command line argument is parsed as an integer and passed to each of the functions you have to implement and the results are printed to stdout. The inputs can be specified in decimal, octal, hexadecimal, binary, or as an IPv4 “dotted quad” address like 132.162.201.24. See the examples below.

You will need to implement the following functions.

• fn is_odd(x: i32) -> i32: This method returns 1 if x is odd, and 0 if it is even. It returns 0 on 6, and 1 on 5.

• fn is_negative(x: i32) -> i32: This method returns 0 if x is positive, and 1 if x is negative. It returns 0 on 4, and 1 on -3.

• fn div_by_4(x: u32) -> u32: This methods performs unsigned integer division by 4. It returns 1 on 6, 3 on 13, and 0 on 3.

• fn nearest_odd(x: i32) -> i32: This method rounds up the number to the nearest odd number. It returns 7 on 6, 5 on 5, and -3 on -4.

• fn flip_parity(x: i32) -> i32: This method adds 1 to even numbers, and subtracts one from odd numbers. It returns 7 on 6, 4 on 5, and -4 on -3.

• fn routing_prefix(addr: u32) -> u32: IPv4 network addresses are stored as 32 bit integers. Each address is divided into two parts: the routing address and the host address. The routing address specifies the network the computer is on (for example, Oberlin’s network). The host address identifies a specific computer on that network. A subnet mask is applied to an IPv4 address to zero out bits corresponding to the host address, leaving just the routing prefix.

  Your task is to write a function that returns the routing addresses for a network with 256 host addresses: these routing addresses will consist of the 24 highest order bits of the address, with the last 8 bits of the address set to 0. If you code this function correctly, the IP form of your result should look like x.x.x.0.

• fn make_readable(perms: u32) -> u32: The chmod, or change mode, command in Unix is used to change access permissions. It accepts user permission flags as a 3 digit octal number, where the first digit corresponds to the User permissions, the second digit corresponds to the Group permissions, and the third digit corresponds to the Other permissions. Each octal digit is three bits. For chmod, we set the most significant bit of the digit to 1 to give read permission, the middle bit to 1 to give write permission, and the least significant bit to 1 to give execute permission. For this function, take in a number that represents a set of permissions, and set all the read permission bits to 1. All other permission bits should remain unchanged. Good values for testing are 0, 64 (0o100 in octal, i.e. execute for user and no permissions for anyone else), and 146 (0o222 in octal, or only write permissions set for everyone).

Testing

For each function that you implement, write a unit test containing at least 3 assertions. Your tests should appear in the test module in src/lib.rs. A test function for is_odd is provided for you to use as a template for other tests. You don’t need to add additional tests for is_odd, but you may if you wish.

To run the tests, you can run

$ cargo test --lib

in the terminal.

Examples

Here are some sample outputs when running bitops with different arguments.

$ cargo run --quiet -- 0o640
is_odd(416) = 0
is_negative(416) = 0
div_by_4(416) = 104
nearest_odd(416) = 417
flip_parity(416) = 417
routing_address(416 /* 0.0.1.160 */) = 256 /* 0.0.1.0 */
make_readable(0o640) = 0o644

$ cargo run --quiet -- -87  
is_odd(-87) = 1
is_negative(-87) = 1
div_by_4(4294967209) = 1073741802
nearest_odd(-87) = -87
flip_parity(-87) = -88
routing_address(4294967209 /* 255.255.255.169 */) = 4294967040 /* 255.255.255.0 */
make_readable(0o37777777651) = 0o37777777655

$ cargo run --quiet -- 132.162.201.24
is_odd(-2069706472) = 0
is_negative(-2069706472) = 1
div_by_4(2225260824) = 556315206
nearest_odd(-2069706472) = -2069706471
flip_parity(-2069706472) = -2069706471
routing_address(2225260824 /* 132.162.201.24 */) = 2225260800 /* 132.162.201.0 */
make_readable(0o20450544430) = 0o20450544474

Submission

Submit the lab by committing your code and pushing it to your GitHub repository.

Lab 3. MIPS Fibs

Due: Sunday, March 9 at 23:59

Your task is to write a program which computes an initial portion of a generalized Fibonacci sequence and prints it out. You will write this program in MIPS using the MARS simulator.

Preliminaries

Click on the assignment link.

Once you have accepted the assignment, you can clone the repository on your computer by following the instruction and begin working.

Be sure to ask any questions on Ed.

Program specification

No starter code is provided this time. Create a file in MARS called lab3.asm and create your program there. You may wish to look at your code for Lab 1 for reference.

Input

Read three input values from the keyboard:

1. the first number in the sequence,
2. the second number in the sequence, and
3. the number of elements of the sequence.

Each element of the sequence (beyond the first two) is equal to the sum of the previous two. For example, if the user inputs 3, 1, and 10, then your program should generate the sequence 3, 1, 4, 5, 9, 14, 23, 37, 60, 97.

Output

For each element of the sequence that you generate, display

• the number in decimal notation (using system call 1),
• the number in hexadecimal, and
• the number of 1-bits in the binary representation of the number.

For the example above, you would display the following.

3 0x00000003 2
1 0x00000001 1
4 0x00000004 1
5 0x00000005 2
9 0x00000009 2
14 0x0000000E 3
23 0x00000017 4
37 0x00000025 3
60 0x0000003C 4
97 0x00000061 3

The hex version can be displayed using system call 34.

Implementation

To get full credit for this assignment, you will need to create a function to count the number of ones in a number. You should use proper calling conventions as discussed in class. You will also need to use a loop to generate the generalized Fibonacci numbers.

You will not need to use either arrays or recursion for this problem. You are required to write a separate function which counts the number of ones in a number. (Hint: Think about using bit operations to isolate each bit in the number, and add them together.)

Make sure to document your programs thoroughly. (This is especially important in assembly language programs, since the code itself is less easily read than high-level language code.) This should include:

• A block of comment lines at the beginning of the source file, giving the name and author of the program and a black-box description of what it does.
• A few comment lines between major sections of the program, describing the contents of each section.
• A comment at the end of most source lines, describing what the instruction on that line does.

Helpful resources

• A guide to the MARS simulator
• A list of MIPS system calls

Submission

Submit the lab by committing your code and pushing it to your GitHub repository.

Lab 4. MIPS Array

Due: Sunday, March 16 at 23:59

Your task is to write a program to read a list of (x,y) pairs representing points in the xy-plane and print them in ascending order, according to their distance from the origin. You will write this program in MIPS using the MARS simulator

Preliminaries

Click on the assignment link.

Once you have accepted the assignment, you can clone the repository on your computer by following the instruction and begin working.

Be sure to ask any questions on Ed.

Program specification

No starter code is provided this time. Create a file in MARS called lab4.asm and create your program there. You may wish to look at your code for Lab 3 for reference.

Input

The first line of input is an integer $n$ (with $1\le n\le 1000$) representing the number of points in the list. This is followed by $2n$ additional lines of input containing the coordinates of the points to be sorted. For example, the list $\{(3,4),(4,2),(0,-5),(1,3)\}$ would be input as:

4
3
4
4
2
0
-5
1
3

You can read the values using system call 5 (read integer). (System call 5 requires that only one integer appear on each line.)

The input should be stored in an array. You can view the storage conceptually as a series of pairs, as shown below.

3  4
4  2
0 -5
1  3

Output

The output of the program will consist of $n$ lines, each containing the x- and y-coordinates of one point in the sorted list. For example, the output from the list of 4 points shown above would be the following.

1    3
4    2
0    -5
3    4

Implementation

You will need to

• allocate space for the data on the heap using sbrk;
• decide how to map the data to the space you allocate; and
• determine how to address the x- and y-coordinates of each point.

Once you have read in all the data, you need to sort it in increasing order according to the value of $x^2+y^2$; that is, the square of the distance from the point to the origin. If two points in your list are the same distance from the origin, they should be sorted in lexicographic order; that is, first in increasing order according to the x-coordinate, and if the x-coordinates are the same, then according to the y-coordinate. If the same point appears more than once in the input, it should appear with the same multiplicity in the output. For example, the correct ordering of the points $(0,-5)$, $(3,4)$, $(4,-3)$, $(-3,4)$, $(-5,0)$ would be $(-5,0)$, $(-3,4)$, $(0,-5)$, $(3,4)$, $(4,-3)$.

You may use any sort method that you choose. I would recommend using something simple like insertion sort. Keep in mind that when you swap two points in your list, you must swap both their x- and y-coordinates.

You may assume that overflow will not occur as a result of computing $x^2+y^2$.

For full points, you must structure your solution to use functions. See the next section for the required list of functions. Functions must be proper functions with arguments passed in the argument registers, results returned in the return registers, caller-saved registers that are used must be saved before use and restored before returning.

Plan for developing the program

First, write and debug a program that will read $n$ and the list of points, store each point in the array, and print it in the desired format.

After that, go back and add the sort operation. Make sure to test!

You will need to write the following functions.

1. (5 pts) A main function that reads the number of points from the user, allocates enough space to hold the points (each point is two integers) and then calls three functions, read_points, sort_points, and print_points. It ends by calling the exit system call.
2. (5 pts) A read_points function that takes a pointer to the array of points and the number of points. In a loop, it reads the x- and y-coordinates for each point and stores them in the array.
3. (9 pts) A sort_points function that takes a pointer to the array of points and the number of points. I used one of the $O(n^2)$ sorting algorithms you learned about in 150 rather than something faster like Quicksort or Mergesort. The sort_points function needs to determine if one point is “smaller” than another. To that end, sort_points calls a point_less_than function whenever two points need to be compared. Many sorting algorithms are built on the idea of swapping two elements so you will write a swap function that swaps two elements.
4. (8 pts) point_less_than takes two pointers as arguments. The first pointer points to the first point and the second to the second point. Since each point is just two consecutive integers, if p were a pointer to a point, then (in C), p[0] is the x-coordinate and p[1] is the y-coordinate. In MIPS, since $a0 will be the argument register holding the first pointer, we can access the x- and y-coordinates as follows.

   lw      $t0, 0($a0) # load the x-coordinate of the first point into $t0
   lw      $t1, 4($a0) # load the y-coordinate of the first point into $t1
   

   point_less_than returns 1 if its first argument is less than its second; otherwise, it returns 0.
5. (8 pts) Like point_less_than, swap takes two pointers to points as arguments. It loads the four integers (two for each point), and then stores them in the appropriate location for the other point.
6. (5 pts) A print_points function which prints the points in a loop.

Each of these 6 functions must be a proper function meaning arguments are passed in $a0 through $a3 and the return value (if any) is in $v0. Proper stack manipulation must be performed (reserving space on the sack for registers, including $ra in the prologue and cleaning it up in the epilogue).

Writing proper functions

You may initially find writing proper functions to be a hassle, but doing so will make your code vastly easier to read and reason about. And it’s required to get full points.

I recommend reviewing the slides for “Procedures” and “The stack” on the course website for details on how to correctly construct a stack frame. Briefly, every non-leaf function needs to allocate a stack frame that contains space for local variables and temporaries, saved registers (like $ra and $s0), and at least space for 4 words of “argument build area” (which the called function can use to save the argument registers). Stack frames should be a multiple of 8-bytes in size. See the below figure from the MIPS ABI.

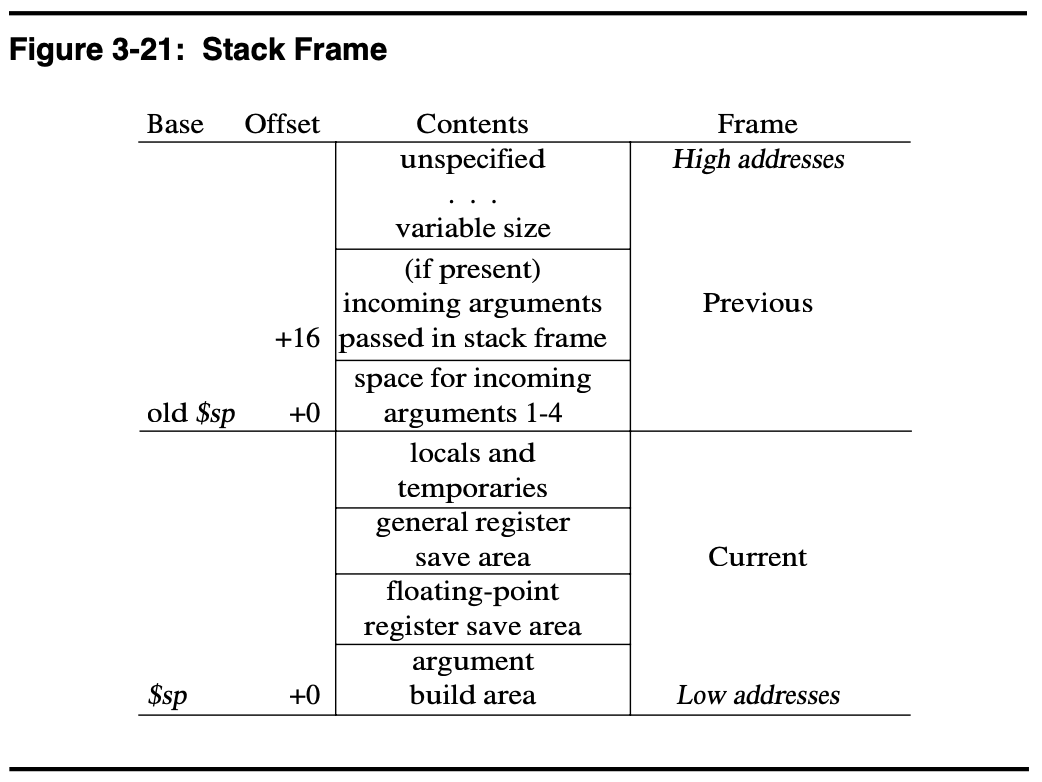
When figuring out the size of the stack frame for a function, count how many registers you need to save (which will be at least one for $ra), add 4 for the “argument build area” and round up to a multiple of 2. This gives you how many words you need to allocate for the stack frame. Multiplying by 4 gets you the number of bytes to decrement the stack pointer. For example, a non-leaf function which only needs to preserve $ra requires a stack frame of size $round\_up(1+4)\cdot 4=24$ bytes.

Finally, the MARS simulator initializes the stack frame to a multiple of 4, but not a multiple of 8. A neat trick to round a positive number (like an address) down to the nearest multiple of a given power of 2 is to AND the number with the negative of the power of two. In this case, we want to round $sp down to the nearest multiple of 8 so we can use

li    $t0, -8
and   $sp, $sp, $t0

as the first two instructions in main to get an 8-byte aligned stack pointer. After these two instructions, you’ll want to decrement the stack pointer to allocate a stack frame for main.

Helpful resources

• A guide to the MARS simulator
• A list of MIPS system calls

Submission

Submit the lab by committing your code and pushing it to your GitHub repository.

Lab 5. 7-segment display

Due: Sunday, March 30 at 23:59

In this assignment, you will design a combinational logic circuit which will control a 7-segment LED display, which looks like this.

Preliminaries

We will be using the CircuitVerse website to complete this assignment. You should have received an email inviting you to the “CSCI 210 Spring 2025” group on CircuitVerse. If you did not, please use this link to join the group. To start the assignment, click on your name on the upper righthand side of the website. Go to “My Groups” and then select the group for this class and you should see “Lab 5” under assignments. Click the “Start Working” button to start the assignment. After you click “Start Working” you can click “Launch Simulator” to start creating the assignment.

You can find more details on how to use the CircuitVerse website here.

4-16 Decoder

You’re going to use a 4-16 decoder in order to implement the 7-segment display controller. As a subcircuit, implement a 4-16 decoder. It should have 4 input lines representing a number from 0 to 15 and it should have 16 output lines. At any given moment, exactly one output line must be 1 and the other 15 must be 0.

7-Segment Display Controller

The input to circuit is a set of 4 signals a3, a2, a1, a0 representing the digits of a 4-bit binary number. The output is a set of the seven signals a, b, c, d, e, f, and g used to drive the seven segments of the LED display. When implemented correctly, your circuit will display value of the input as a hexadecimal digit on the 7 segment display. Below is the display with each segment labeled.

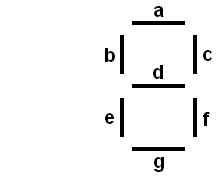
Your display controller should pass its 4 inputs to the 4-16 decoder you constructed and the output of the decoder should be used to drive the seven LED signals.

Each of the LED signals can be represented as a simple boolean function of the 16 decoder outputs. For example, if the input is 0101, the output of the decoder should be a single 1 which turns on segments a, b, d, f, and g, while c and e are off, forming the digit “5” on the display.

You should implement all 16 hexadecimal digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, b, C, d, E, and F. (Note that b and d are lower case to distinguish them from 8 and 0.)

Implementation plan

You should use the following plan for implementing this lab.

1. Draw out all the numbers on graph paper first.
2. For each of the segments a–g, write down which numbers correspond to that segment.
3. Build a 4-bit decoder as a subcircuit. You MUST have your decoder as a subcircuit in order to receive full credit for this lab. Documentation for how to create a subcircuit is here.
4. For each segment, create one or more OR gates (as needed), add the appropriate outputs from the decoder to the OR gate.
5. Keep wires straight or right-angle turns. Pick the order the decoder outputs will go into the OR gates so as to minimize wire crossing.
6. If inadvertent connections are made, undo, don’t try to fix it.

Performing step 2 before step 4 is critical. You don’t want to be trying to wire this up while figuring out which decoder outputs you need to OR.

Submission

Make sure to select the “save online” button to save your project. This will make your project available to us for grading.

Lab 6. Adder/Subtracter

Due: Sunday, April 6 at 23:59

In this lab, you will build an eight-bit adder/subtracter.

Preliminaries

We will be using the CircuitVerse website to complete this assignment. To start the assignment, click on your name on the upper righthand side of the website. Go to “My Groups” and then select the group for this class and you should see “Lab 6” under assignments. Click the “Start Working” button to start the assignment. After you click “Start Working” you can click “Launch Simulator” to start creating the assignment.

You can find more details on how to use the CircuitVerse website here.

Lab 7. Four-bit Counter

Due: Sunday, April 13 at 23:59

In this lab, you will build an four-bit counter out of J-K flip-flops. To build the J-K flip-flops, you’re going to build a clocked S-R latch.

Preliminaries

We will be using the CircuitVerse website to complete this assignment. To start the assignment, click on your name on the upper righthand side of the website. Go to “My Groups” and then select the group for this class and you should see “Lab 7” under assignments. Click the “Start Working” button to start the assignment. After you click “Start Working” you can click “Launch Simulator” to start creating the assignment.

You can find more details on how to use the CircuitVerse website here.

Clocked S-R latch

You should first build a clocked S-R Latch as a subcircuit. Lectures 18 and 19, as well as Appendix B.8 of the textbook should be helpful to you here. The S-R latch must be a subcircuit to get full credit for the lab.

Your subcircuit should take in inputs S, R and C (for clock), and have outputs Q and Q. When C is 1, the outputs Q and Q are controlled by S and R. When C is 0, the outputs should not change regardless of the values of S and R. (Note that for this subcircuit, you should make the clock an input value, and not actually hook up the clock to the circuit.)

The S-R latch must be a subcircuit to get full credit for the lab.

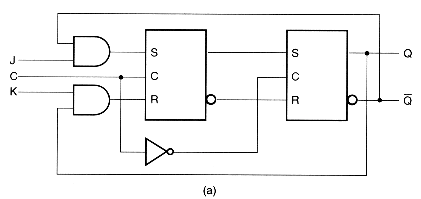
J-K flip-flop

Next you will build a J-K flip-flop out of two clocked S-R latches. Your subcircuit inputs should be J, K and C (for clock again), and your output should be Q. The J-K flip-flop must be a subcircuit in order to get full credit for the lab. Below is a circuit diagram for a J-K flip-flop. (Please note that the circles on the Q output of this diagram are just to indicate that the output is the inverse of the Q output; they don’t mean that Q is being inverted to be the same as Q!)

Counter

Your main circuit is a four-bit counter which you will build out of four J-K flip-flops.

This circuit should not require any input from the user/viewer of the circuit; you should use the clock as input, and it should automatically make your counter increase by one for every clock cycle. Your output should be a binary number displaying the current count. You can either display this as 4 individual 1-bit outputs, or 1 four-bit output. Your counter should count through 0000, 0001, 0010, 0011, …, 1110, 1111 and then start over at 0000.

Let’s start by considering a 1-bit counter. Every clock cycle, the output should alternate between 0 and 1. See the timing diagram below. Notice how output $X_0$ alternates between 0 and 1 and it stays at each of those for an entire clock period (the interval between the blue lines).

Look at Problem Set 8. There is a particular configuration of inputs to a J-K flip-flop that causes the output to “toggle” between 0 and 1 every time its clock input, C, changes from 1 to 0. Using a single J-K flip-flop, you can construct a 1-bit counter.

Next, let’s build a 2-bit counter. This should count as 00, 01, 10, 11, 00. Notice that the least-significant bit, $X_0$, toggles on every clock cycle but $X_1$ only toggles when $X_0$ changes from a 1 to a 0, not when the clock changes from a 1 to a 0. In the image below, the blue vertical lines correspond to the counter values 00, 01, 10, 10, 11, 00, from left to right.

To get a 2-bit counter, we just need two J-K flip-flops with appropriate J and K values and with the clock input of the second J-K flip-flop being the output from the first flip-flop.

Similarly, we can build a 3-bit counter by adding another flip-flop. Look at the timing diagram below. When does $X_2$ toggle?

We can continue this process to get a 4-bit counter.

Implementation plan

You are required to build this counter using only with basic logic gates (i.e., AND, OR, NOT, NOR, NAND and XOR). You are not allowed to use the CircuitVerse latches and flip-flops. You should take the following steps.

1. Build an S-R latch as a subcircuit;
2. Build a J-K flip-flop as a subcircuit; and
3. Build a four-bit counter out of four J-K flip-flops.

You are required to have a separate S-R latch and J-K flip-flop subcircuits to get full credit for the lab. You must build your own J-K flip-flops and S-R latches. Using the CircuitVerse latches or flip-flops will result in a failing grade for this lab.

Submission

Make sure to select the “save online” button to save your project. This will make your project available to us for grading.

Lab 8. Floating Point

Due: Sunday, April 27 at 23:59

XXX: This is the old version of the lab which will be updated this semester

In this lab, you will implement part of the IEEE 754 Standard for Floating-Point Arithmetic. In particular, you will implement single precision (32-bit) floating point addition and multiplication.

Preliminaries

You may discuss your implementation with a partner; however, each of you needs to write and submit your own code. So no copying and pasting, but you should feel free to work together on a solution and to debug.

Click on the assignment link.

Once you have accepted the assignment, you can clone the repository on your computer by following the instruction and begin working.

Be sure to ask any questions on Ed.

Program Specification

In the assignment repo, you’ll find a single Java file, Xfloat.java which defines an Xfloat class. This class represents a single-precision floating point number with the following members.

private byte sign;
private byte exponent;
private int significand;

Of course, these represent the three fields of a floating point number.

The file also contains a main method that takes two floats as command-line arguments and prints them out along with the product and sum of the numbers. For example, running the program with floats 2.5 and 7.25 gives this output.

$ java Xfloat 2.5 7.25
x:   40200000 (0 10000000 01000000000000000000000) sign: 0 exp: 80 sig: 200000 2.5
y:   40E80000 (0 10000001 11010000000000000000000) sign: 0 exp: 81 sig: 680000 7.25
x*y: 00000000 (0 00000000 00000000000000000000000) sign: 0 exp: 00 sig: 000000 0.0
x+y: 00000000 (0 00000000 00000000000000000000000) sign: 0 exp: 00 sig: 000000 0.0

The first 8 hex-digit number corresponds to the bits of the actual IEEE floating point number. The binary representation follows, separated into sign, exponent and significand fields. Next are the corresponding Xfloat fields in hex. Note that the significand field requires only 6 hex digits since only 23 of the 32 bits are actually used.

You only need to implement two methods.

public static Xfloat xadd(Xfloat x, Xfloat y) : Add Xfloats x and y together and return the result.

public static Xfloat xmult(Xfloat x, Xfloat y) : Multiply Xfloats x and y together and return the result.

You must implement the methods by performing the addition/multiplication by operating on the three fields of each Xfloat.

You should not modify any other methods.

You may ignore subnormal numbers, infinities, and NaN, but you must properly handle 0.0.

You must use bit masking and shifting to manipulate bits. In particular, you are not allowed to convert your integers to strings.

Hints

• When implementing xadd, you’ll need to shift the significand of the number with the smaller magnitude so that the two numbers have the same exponent. However, if the number of bits you need to shift by is greater than 31, you should just set the significand to rather than trying to shift by more than 31. This is because val >> 32 in Java is the same thing as val and val >> 33 is the same as val >> 1. In general if shamt >= 32, then val >> shamt is the same as val >> (shamt % 32) which can lead to surprising results.

  For example, when adding 0.000000237 and 234624.0, the exponent for the first is $-23$ and the exponent for the second is 17. To make the first have the same exponent as the second, we’d need to shift the first’s significand right by $17--23=40$. In this case, the final result should be 234624.0.

• When implementing xmult, you’ll need to multiply the significands. You should perform the following steps.

  1. Convert the significands to 64-bit longs;
  2. Use Xfloat.HIDDEN_BIT to add the hidden bit to the significands;
  3. Multiply the two 64-bit significands;
  4. Shift the result appropriately (making necessary adjustments to the exponent); and
  5. Cast the significand back to 32 bits and remove the implicit 1.

• The various XXX_MASK constants defined in Xfloat may be helpful.

• In Java, the unsigned right shift operator is >>>.

• Because Java only uses signed numbers, you may want to use types that are larger than the ones you need. For example, you will probably want to work with the exponents by assigning them to ints before working with them. Something like

  int e = x.exponent & 0xFF;
  

  will give you x’s exponent as an integer in the range [0, 255]. If you omit the & 0xFF, then any x.exponent that’s larger than 127 will give you a negative number.

• Check out the page of worked examples.

Tests

Included in the repository is a Python test script, test.py. This script will compile and test your code against 10 fixed inputs or, if you pass the -r option to it, against an additional 100 randomly chosen inputs.

$ ./test.py
Compiling
x=0.0 y=0.0: PASS
x=-1.0 y=0.0: PASS
x=0.0 y=-1.0: PASS
x=0.9 y=0.1: PASS
x=1.5 y=1.5: PASS
x=6.66666 y=3.3333333: PASS
x=2.25 y=0.5: PASS
x=-4.0 y=2.0: PASS
x=-20486.0 y=-2.5e-06: PASS
x=4.70197740328915e-38 y=2.1267647932558654e+37: PASS
10/10 tests passed

Or

$ ./test.py -r
Compiling
x=0.0 y=0.0: PASS
x=-1.0 y=0.0: PASS
x=0.0 y=-1.0: PASS
x=0.9 y=0.1: PASS
x=1.5 y=1.5: PASS
x=6.66666 y=3.3333333: PASS
x=2.25 y=0.5: PASS
x=-4.0 y=2.0: PASS
x=-20486.0 y=-2.5e-06: PASS
x=4.70197740328915e-38 y=2.1267647932558654e+37: PASS
10/10 tests passed

Performing 100 random tests
x=-1.5824437428766114e+19 y=7.654288931433146e-16: PASS
x=-519727136.0 y=-4.693174584159976e+27: PASS
x=5.338058977860687e-34 y=-110286184.0: PASS
...
x=-1.7480781718172477e-25 y=3.453274344019857e+34: PASS
100/100 random tests passed

Submission

Submit the lab by committing your code and pushing it to your GitHub repository.

Lab 8. Floating Point examples

XXX: This is the old version of the lab which will be updated this semester

Lab 8 asks you to implement addition and multiplication for single-precision, 32-bit floating point numbers. A few worked examples are given below.

Addition

My implementation for xadd looks something like this.

1. Check if either x or y is zero and return the other one if so;
2. Denormalize x or y to give them the same exponent (the exponent of the larger one);
3. Add the significands, taking sign into account;
4. If the result is 0, return 0;
5. Normalize the result; and
6. Encode the result (bias the exponent; and mask off the hidden bit) and finally construct the new Xfloat with the result’s sign, exponent, and significand.

Let’s apply this algorithm to adding $2.5$ and $-7.25$ to see how this works.

Let’s start by encoding these as a 32-bit single precision floating point number, performing the 5 steps, and looking at the result.

$2.5_{10}=10.1_2=1.01_2\cdot 2^1=(-1{)}^0\cdot 1.01000000000000000000000_2\cdot 2^1$. Therefore, the three fields of the float are sign = 0, exponent = 1, and significand = $1.01000000000000000000000_2$. These are encoded as 0 10000000 01000000000000000000000 (where I’ve added 127 to the exponent and dropped the hidden bit from the significand).

$-7.25_{10}=-111.01_2=(-1{)}^1\cdot 1.11010000000000000000000_2\cdot 2^2$. Therefore, the three fields of the float are sign = 1, exponent = 2, and significand = $1.01000000000000000000000_2$. Similarly, these are encoded as 1 10000001 11010000000000000000000.

Step 1. Neither x nor y are zero, so we continue to step 2.

Step 2. Extract and unbias the exponents for x and y; extract and add in the hidden bit to the significands for x and y. This gives the following.

x_exp = 1
y_exp = 2
x_sig = 00000000 1 01000000000000000000000
y_sig = 00000000 1 11010000000000000000000

In x_sig and y_sig, the first 8 bits are 0s, the next bit is the hidden 1 bit and the remaining 23 are the significand without the hidden bit.

Since y_exp > x_exp, we denormalize x by shifting x_sig right by y_exp - x_exp and setting x_exp to y_exp. This gives us the following variables.

x_exp = 2
y_exp = 2
x_sig = 00000000010100000000000000000000
y_sig = 00000000111010000000000000000000

Step 3. We need to add the significands together paying attention to the sign. Because x is positive and y is negative, we need to compute z_sig = x_sig - y_sig where z is going to be the result. In this case, z_sig is negative and we can’t have that, so we’ll set z_sign = 1 and z_sig = -z_sig. In any case, z_exp = x_exp = y_exp, although that can change in step 5 when we normalize the result.

z_sign = 1
z_exp = 2
z_sig = 00000000100110000000000000000000

Step 4. The result is not zero, so move to the next step.

Step 5. Now, we need to normalize the result, but in this particular case, there’s actually nothing to be done! I can tell there’s nothing to be done because the significand is 00000000 1 00110000000000000000000. In other words, it starts with eight 0s and then a 1 (the hidden bit) followed by 23 bits. If it started with fewer than eight 0s, we’d need to shift the significand to the right and increment the exponent until it started with eight 0s. If it started with more than eight 0s, we’d need to shift the significand to the left and decrement the exponent until it started with eight 0s.

This gives our final value of

z_sign = 1
z_exp = 2
z_sig = 00000000 1 00110000000000000000000

We can check we did this correctly with some arithmetic: $(-1{)}^1\cdot 1.0011_2\cdot 2^2=-100.11_2=-4.75$. Success!

Step 6. The last thing we need to do is encode the result. So we need to add 127 to the exponent and mask off the hidden bit in the significand giving 1 10000001 00110000000000000000000.

The previous example shows off all of the steps except for step 5, normalize the result. So let’s do another quick example, but this time using 2.5 and 7.25.

Steps 1 and 2 are identical. After them, we have

x_exp = 2
y_exp = 2
x_sig = 00000000010100000000000000000000
y_sig = 00000000111010000000000000000000

In step 3, we simply add the significands together since neither x nor y is negative. This gives.

z_sign = 0
z_exp = 2
z_sig = 00000001001110000000000000000000

Step 4 is the same: z_sig is not 0, so we continue to step 5.

Step 5. Here, z_sig starts with seven 0s so we need to shift z_sig right by 1 and increment the exponent by one giving

z_sign = 0
z_exp = 3
z_sig = 00000000 1 00111000000000000000000

Checking our arithmetic, we have $(-1{)}^0\cdot 1.00111_2\cdot 2^3=1001.11_2=9.75$. Success!

Step 6. We encode by adding 127 to the exponent and masking off the hidden bit as before giving 0 10000010 00111000000000000000000.

Multiplication

My implementation of xmult looks something like this.

1. If either x or y is 0, return 0;
2. Compute the sign of the result;
3. Add the exponents;
4. Multiply the significands and shift;
5. Normalize the result; and
6. Encode the exponent and significand.

As a simple example, let’s multiply $-1$ and $33.25$. These have encodings

x: 1 01111111 00000000000000000000000
y: 0 10000100 00001010000000000000000

Step 1. Neither x nor y are 0, so continue to step 2.

Step 2. Since x is negative and y is positive, we know the result is negative.

z_sign = 1

Step 3. Add the exponents. Since the exponent of x is 0 and the exponent of y is 5, the exponent of the result is 5.

z_exp = 5

Step 4. Multiply the significands as 64-bit longs, don’t forget the hidden bits!

x_sig = 00000000 00000000 00000000 00000000 00000000 10000000 00000000 00000000
y_sig = 00000000 00000000 00000000 00000000 00000000 10000101 00000000 00000000
z_sig = 00000000 00000000 01000010 10000000 00000000 00000000 00000000 00000000

The significands of x and y aren’t really $100000000000000000000000_2$ and $100001010000000000000000_2$, they’re actually $1.00000000000000000000000_2$ and $1.00001010000000000000000_2$ (note the binary point). That is, the real significands are the 24-bit values (23 bits from the float plus the hidden bit) multiplied by $2^{-23}$. And when we multiply them together, our result is really $$0000000000000000010000101000000000000000000000000000000000000000_2\times 2^{-46}.$$

To bring the result back to our normal representation as a number times $2^{-23}$, we need to shift z_sig right by 23 bits.

z_sig = 00000001 00001010 0000000 00000000

Steps 5 and 6, normalizing and encoding the result work the same as for addition.

In this case, there’s nothing to be done, z_sig is already normalized (as a 32-bit integer, it has 8 leading zeros followed by the 1 corresponding to the hidden bit). Thus, our result is $(-1{)}^1\cdot 1.0000101_2\times 2^5=-100001.01_2=-33.25$ and its encoding is 1 10000100 00001010000000000000000.

Final: Cache simulation

Due: Friday, May 16 at 11:00

XXX: This is the old version of the lab which will be updated this semester.

For this final project, you will write a configurable cache simulator using the infrastructure provided. Your cache simulator will read an address trace (a chronological list of memory addresses referenced), simulate the cache, generate cache hit and miss data, and calculate the execution time for the executing program. The address traces have been generated by a simulator executing real programs. Your cache simulator will be graded for accuracy, but is not the end product of this project, rather it is a tool you will use to complete the project. In this project, you will experiment with various cache configurations and make conclusions about the optimal cache organization for this set of programs.

Preliminaries

You can work on this project with a partner if you choose. If you decide to work with a partner, you and your partner should check out a single repository. The first partner will create a team name, and the second partner should choose that team name. Please be careful choosing a team, as this cannot be undone. Please name your team something that makes it clear who you are.

If you choose to work with a partner, you and your partner must complete the entire project together. Dividing the project up into pieces and having each partner complete a part of it on their own will be considered a violation of the honor code. Both you and your partner are expected to fully understand all of the code you submit.

Click on the assignment link.

Once you have accepted the assignment, you can clone the repository on your computer by following the instruction and begin working.

Be sure to ask any questions on Ed.

Address trace

An address trace is simply a list of addresses produced by a program running on a processor. These are the addresses resulting from load and store instructions in the code as it is executed. Some address traces would include both instruction fetch addresses and data (load and store) addresses, but you will be simulating only a data cache, so the provided traces in the traces directory only have data addresses.

These traces were generated by a simulator of a RISC processor running three programs, art, mcf, and swim from the SPEC benchmarks. The files are art.trace.gz, mcf.trace.gz, and swim.trace.gz. The number of loads/stores in the traces vary by benchmark. They are all compressed with gzip. You do not need to decompress the traces because Cache.java knows how to read both compressed and uncompressed files. (In addition, there is a test.trace file containing the contents of the example trace shown below.)

Use the following command to run your simulator on the given trace file.

$ java Cache [cache args] tracefile

Because your workload is three programs, you will run three simulations for each architecture you simulate, and then combine the results in some meaningful way. The simulator arguments should be taken in as command line arguments. For example, to simulate a 32 kB, 4-way set-associative cache with 32-byte blocks and a 30-cycle miss penalty on the traces/mcf.trace.gz trace file, you’d run the following.

$ java Cache -s 32 -a 4 -b 32 -mp 30 traces/mcf.trace.gz

Your code should support any reasonable values for cache size, associativity, etc.

Format of the address trace

All lines of the address trace are of the format

# LS ADDRESS IC

where LS is a 0 for a load and 1 for a store, ADDRESS is an 8-character hexadecimal number, and IC is the number of instructions executed between the previous memory access and this one (including the load or store instruction itself). There is a single space between each field. The instruction count information will be used to calculate execution time (or at least cycle count). A sample address trace starts out like this:

# 0 7fffed80 1
# 0 10010000 10
# 0 10010060 3
# 1 10010030 4
# 0 10010004 6
# 0 10010064 3
# 1 10010034 4

You should assume no accesses address multiple cache blocks (e.g., assume all accesses are for 32 bits or less and appropriately aligned).

Simulator (40 points)

Your simulator will model an n-way set associative, write-back, write-allocate cache. The cache replacement policy is always least-recently used for associative caches.

When run on a trace file, it should produce

• total execution time in cycles;
• number of instructions;
• number of memory access instructions (i.e., number of loads and stores);
• overall cache miss rate;
• cache miss rate for load instructions;
• cycles per instruction (CPI);
• average memory access time in cycles (cycles per memory access, assuming 0 cycles for a cache hit and a miss penalty for a cache miss; see below);
• the number of dirty cache blocks evicted;
• the number of load misses;
• the number of store misses;
• the number of load hits; and
• the number of store hits.

See the examples below.

For execution time, assume the following.

• Instructions other than loads and stores take one cycle;
• A load or store takes one cycle plus a miss penalty if applicable;
• A load or store that misses in the cache has a configurable miss penalty with a default of 30 cycles;
• A load or store that misses in the cache and causes the cache to evict a dirty cache block has an additional 2 cycle penalty.

(We’re assuming that on a cache miss that causes a dirty block to be evicted, the write back to memory happens mostly in the background and the additional 2-cycle penalty is to write the dirty block to a write buffer.)

To recap: With the default base miss penalty of 30 cycles, a load or store instruction takes 1 cycle for a cache hit, 30 cycles for a cache miss that does not evict a dirty block, and 32 cycles for a cache miss that evicts a dirty block.

In the trace shown above, the first 31 instructions take 151 cycles, assuming four cache misses and 3 cache hits for the 5 loads and 2 stores, and a 30-cycle base miss penalty.

Each trace contains the memory accesses of just over 5 million instructions. Your simulations should process all of them. Your output must follow the format provided in the skeleton code exactly. See the examples below.

Questions (40 points)

For the second part of this project, you will use your cache simulator to test out different cache configurations and answer questions about your findings. You must try every configuration below on the art, swim, and mcf cache traces provided to you, and discuss all of them in your answers to the questions. Note that your question answers are worth just as much as the code for this project—you are expected to give detailed answers that clearly backup your claims with your simulator results.

The default cache configuration will be 16-byte block size, direct-mapped, 16 kB cache size, write-back, and write-allocate. You will re-evaluate some of these parameters one at a time, in the given order. In each case, choose a best value for each parameter, then use that for all subsequent analyses.

Look at 16 kB, 32 kB, and 128 kB cache sizes. Larger caches take longer to access, so assume that a processor with a 32 kB cache requires a 5% longer cycle time, and the 128 kB 15% longer. Choose the best size/cycle time combination and proceed to the next step.

Look at cache associativity of direct-mapped, 2-way set-associative, and 8-way set-associative. Assume that 2-way associative adds 5% to the cycle time, and 8-way adds 10% to the cycle time. Choose the best associativity and cycle time, and proceed to the next step.

Look at cache block sizes of 16, 32, and 64 bytes. Assume that it takes two extra cycles to load 32 bytes into the cache, and 6 extra cycles to load 64 bytes. (i.e., raise the miss penalty accordingly). Choose the best size and miss penalty and proceed to answering the following questions.

1. (10 points) What is the optimal cache size, associativity, and block size, given the parameters above?
2. (10 points) Is the cache miss rate a good indicator of performance? In which cases did the option with the lowest miss rate not have the lowest execution time? Why?
3. (10 points) Were results uniform across the three programs? In which cases did different programs give different conclusions? Speculate as to why that may have been true.
4. (10 points) What was the speedup of your final design over the default for each trace? Use the definition of speedup covered in class.

Put the answers to these questions in the README file.

Hints

Think about how to intelligently debug and test your program. Running immediately on the entire input gives you little insight on whether it is working (unless it is way off). To do this create separate memory tests (you can see the text format above) to ensure cache size, cache associativity, block size, and miss penalty are functioning correctly. You do not need to turn them in, but they will help tremendously.

Speed matters. These simulations should take less than a couple minutes (actually, much less) on an unloaded machine. If it is taking much more than that, do yourself a favor and think about what you are doing inefficiently.

Simulations are not the same as hardware. If your tag only takes 16 bits, feel free to use an integer for that value. Other time-saving optimizations along these lines might be useful.

Submission

Submit the project by committing your code and answers to the questions and pushing it to your GitHub repository.

Examples

Here are three example simulation runs and the command line to produce them. Your output should be identical.

$ java Cache -s 32 -a 4 -b 32 -mp 30 traces/test.trace 
Cache parameters:
    Cache Size (kB)             32
    Cache Associativity          4
    Cache Block Size (bytes)    32
    Miss penalty (cycles)       30

Simulation results:
    execution time                    151 cycles
    instructions                       31
    memory accesses                     7
    overall miss rate                0.57
    load miss rate                   0.60
    CPI                              4.87
    average memory access time      17.14 cycles
    dirty evictions                     0
    load_misses                         3
    store_misses                        1
    load_hits                           2
    store_hits                          1

$ java Cache -s 32 -a 4 -b 32 -mp 30 traces/art.trace.gz
Cache parameters:
    Cache Size (kB)             32
    Cache Associativity          4
    Cache Block Size (bytes)    32
    Miss penalty (cycles)       30

Simulation results:
    execution time               20127356 cycles
    instructions                  5136716
    memory accesses               1957764
    overall miss rate                0.25
    load miss rate                   0.27
    CPI                              3.92
    average memory access time       7.66 cycles
    dirty evictions                 60015
    load_misses                    475672
    store_misses                    20015
    load_hits                     1256211
    store_hits                     205866

$ java Cache -a 8 -s 64 -b 32 -mp 42 traces/mcf.trace.gz
Cache parameters:
    Cache Size (kB)             64
    Cache Associativity          8
    Cache Block Size (bytes)    32
    Miss penalty (cycles)       42

Simulation results:
    execution time              143963250 cycles
    instructions                 19999998
    memory accesses               6943857
    overall miss rate                0.42
    load miss rate                   0.36
    CPI                              7.20
    average memory access time      17.85 cycles
    dirty evictions                995694
    load_misses                   2036666
    store_misses                   867426
    load_hits                     3552806
    store_hits                     486959